So far, I've told you a little about where I believe quantum theory comes from. To briefly recap, information-theoretic incompleteness, a feature of every universal system (where 'universal' is to be understood in the sense of 'computationally universal'), introduces the notion of complementarity. This can be interpreted as the impossibility for any physical system to answer more than finitely many questions about its state -- i.e. it furnishes an absolute restriction on the amount of information contained within any given system. From this, one gets to quantum theory via either a deformation of statistical mechanics (more accurately, Liouville mechanics, i.e. statistical mechanics in phase space), or, more abstractly, via introducing the possibility of complementary propositions into logic. In both cases, quantum mechanics emerges as a generalization of ordinary probability theory. Both points of view have their advantages -- the former is more intuitive, relying on little more than an understanding of the notions of position and momentum; while the abstractness of the latter, and especially its independence from the concepts of classical mechanics, highlights the fundamental nature of the theory: it is not merely an empirically adequate description of nature, but a necessary consequence of dealing with arbitrary systems of limited information content. For a third way of telling the story of quantum mechanics as a generalized probability theory see this lecture by Scott Aaronson, writer of the always-interesting Shtetl-Optimized.
But now, it's high time I tell you a little something about what, actually, this generalized theory of probability is, how it works, and what it tells us about the world we're living in. First, however, I'll tell you a little about the mathematics of waves, the concept of phase, and the phenomenon of interference.
Let's start with some pictures. This is a wave:
 |
| Fig. 1: A wave. |
And this is another wave:
 |
| Fig. 2: Another wave. |
 |
| Fig. 3: Two waves. |
The difference between two peaks, or equivalently between two valleys, is called a phase difference. These two waves are completely out of phase: where one has a peak, the other has a valley, and vice versa. This means, if both reflect the value of some physical quantity at a certain location, say sound pressure, or light intensity, or just water depth, the total value of that physical quantity is the sum of both waves -- in this case, the following:
 |
| Fig. 3: No wave. |
Since every value at every point is added to an equal, but oppositely signed value, the complete result is zero. This phenomenon is known as destructive interference: two waves cancel each other out, if they are equivalent in magnitude, but opposite in phase. More generally, waves of differing magnitudes and phases can yield complicated results when they are added. For instance, consider these three waves:
 |
| Fig. 5: Three waves. |
If allowed to interfere -- if superimposed or brought into superposition --, they give rise to this 'wave':
 |
| Fig. 6: New wave. |
It is not so easy to glean the original three waves just from this graph! (However, there exists a mathematical technique, called Fourier analysis, to do precisely that -- even for superpositions of infinitely many waves.)
A useful way to think about waves and their relative phases is in terms of circular motion. Imagine a particle moving around a circle at constant speed. The projection of its motion onto a plane graphed out over time will be a simple wave, and the position of the particle at any given time corresponds to the height of the graph at a corresponding point.
 |
| Fig. 7: A phasor. (Image credit: wikipedia.) |
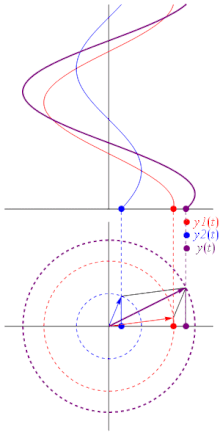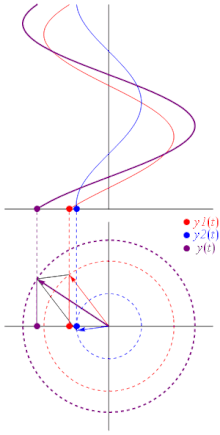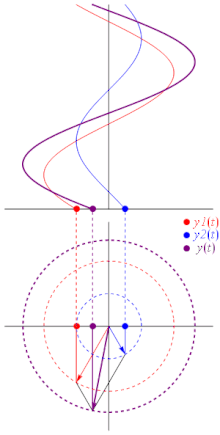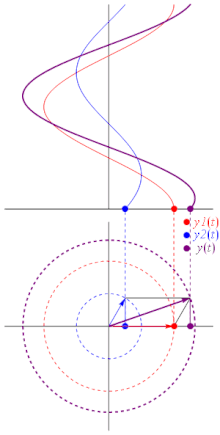 |
| Fig. 8: Interference as a sum of phasors. (Image credit: wikipedia.) |
Wave or particle, or is that the wrong question to ask?
After these preliminary remarks, let's now move on to some physics. It is somewhat customary to introduce quantum theory by considering its historical development -- the explanation for the anomaly in black body spectra by Planck, the application of Planck's idea to the photoeffect by Einstein, Bohr's model of the atom, and so on. However, since this historical development is necessarily somewhat convoluted, involving many false starts and almost-right ideas, this regrettably often leads to a convoluted and almost-right picture of quantum theory. I will thus only consider one single empirical ingredient, and build up the rest through judicious cherry picking of ideas and concepts in a manner that to me appears most logical and clean-cut.
The empirical ingredient I want to consider is the classical double slit experiment. Historically, there had been dissent between two theories on the nature of light: Newton, influenced by Pierre Gassendi, considered light to be made out of particles, or corpuscels ('small bodies'), while Descartes, Hooke, Huygens and others considered light to be a wave, in analogy to sound or water.
As we now know, waves have the unique property of being capable of interference. So it is a natural question to ask whether one can devise an experiment utilizing this effect in order to decide which theory is the right one (interestingly, Newton already had made observations in favor of a wave model of light, in the form of what today are called Newton rings, but had nevertheless held on to his corpuscular model). This turns out to be possible, and at the beginning of the 19th century, Thomas Young carried out an experiment in which he shone light onto a plate with two parallel slits in it, theorizing that if light were a wave, circular waves emanating from the slits would lead to a characteristic interference pattern, while particular light would only illuminate two straight lines as images of the slits, the same way baseballs thrown through two openings would only hit the wall at the points straight behind them.
To understand this, we must now look at two-dimensional waves instead of one-dimensional ones; fortunately, this does not cause any serious new difficulties.
 |
| Fig. 9: Young's double slit experiment. (Image credit: wikipedia.) |
From each of the two slits to some given point on the wall, a wave will undergo a number of oscillations depending on the distance; thus, the wave's amplitude, relative to a wave arriving at the wall from the other slit, will be a function of this distance. As we have learned, at this point, we must then add the amplitudes, and careful reasoning shows that the waves will reinforce at some points, and cancel at others, leading to the characteristic dark-bright-dark pattern in the figure.
When Young carried out his experiment, this pattern was indeed what he saw -- thus, or so it seemed, he had shown that light is indeed a wave, not made out of particles.
However, let's fast forward to modern times, where we have light sources whose intensity can be very accurately tuned. According to the wave model of light, if we successively dim the lights, what we ought to see is a gradual weakening of the interference pattern, until it becomes too faint to observe (we can use various tricks, such as a prolonged exposure on a photographic plate, in order to prolong this time). And at first, this is indeed what we see. But at some point, instead of the continuous, uniform pattern we expect, we see discrete points of illumination, popping up randomly on our photoplate. If we let this build up for a while, we'll get something like this:
 |
| Fig. 10: Long-term exposure with a weak source. (Image credit: wikipedia.) |
This is the origin of what is often called wave-particle duality: sometimes, light seems to behave like a wave, interference and all, while at other times -- especially if we try to sneak a peak at what goes on behind the curtain -- it appears to behave like a particle. This is another example of complementarity, though of a slightly different quality than those we have already encountered.
However, another interpretation is possible. We can look at the situation in terms of probabilities. The probability of one point x of the wall being illuminated is equal to the probability of it being illuminated by light going through slit 1 plus the probability of it being illuminated by light going through slit 2, or: P(x bright) = P(light through S1) + P(light through S2). Clearly, this does not leave room for interference: probabilities are always positive, so for any given point, the sum of both probabilities is strictly greater than either probability alone. We thus get the 'two bright areas' picture we would expect for particles: directly behind each slit, the probability for light to get there via that slit is large, and the probability for it to get there via the other slit is small -- tending to 0 for slits far enough apart; right in the middle, both probabilities will be small (they can again be made arbitrarily small with the right arrangement); behind the other slit, we get the same picture again as behind the first one.
But, as we now know, quantum theory is essentially a generalization of probability theory, so what does it tell us about this situation? Well, first of all, quantum probabilities, as represented by the Wigner density on phase space, can indeed become negative, so it is no longer true that the sum of both probabilities is necessarily larger than either probability on their own. However, one must note that this only happens in such a way that no experiment gives a certain outcome with '-20% probability'! That would be a nonsensical notion, and luckily, these areas are protected against observation by the uncertainty principle.
Even more, though, quantum 'probabilities' -- one typically, for reasons that will become clear soon, talks about 'probability amplitudes' or just amplitudes for short -- can generally take on complex values.
This is very intriguing, because complex numbers have a direct relationship with circular motion. To see this, we must conceive of numbers as being related to transformations. If we have a stick, of length x, with its left end fixed at origin of the number line, i.e. at 0, then any positive real number tells us to stretch that stick by a factor equal to its magnitude, i.e. the number '3' is understood as the instruction 'make the stick three times longer'.
Negative numbers, on the other hand, can be understood as an instruction to flip the stick over, i.e. rotate it by 180° around the origin (remember, the stick is fixed there). So the number '-0.5' tells us to apply a half rotation to the stick, then shrink it to half its previous size. We can also check that this interpretation of numbers gels with our usual one: for instance, applying a half rotation twice is the same as not rotating at all, thus (-1)*(-1) = (-1)2 = 1, as we would expect.
However, why would we limit us to 180° rotations? Let's consider what happens if we rotate our stick by 90°. We have now left the number line, and are in a plane; our stick stands orthogonal to the numbers we considered before. But this is no great mystery -- rotations are quite simple operations. Nevertheless, this simple extension introduces the full formalism of complex numbers. Let's call the number that effects our rotation of 90° i, for convenience. (Clearly, it can't be any of the numbers on the number line, so we have to invent a new name for it.)
Now, the simplest thing in the world is that you rotate by 90° twice (in the same direction), you have in total effected a rotation by 180° -- or, i*i = i2 = -1. Thus, i, somewhat unluckily called the imaginary unit (which can, as we have seen, be tied to the quite real concept of rotation), is the square root of -1. It's a simple concept; nevertheless, it was regarded with suspicion even by mathematicians for centuries.
Anyway, in the end, it turns out that we can represent arbitrary rotations using numbers that are sums of real and imaginary parts, or compositions of stretchings, flips, and 90° rotations. For instance, the number 1 + i corresponds to a 45° rotation:
 |
| Fig. 11: 1 + i in the complex plane. |
This should begin to remind you of something. Indeed, every complex number can be represented by a magnitude and a phase, where the former relates to stretching, the latter to rotation. These phases behave exactly like the ones we're already familiar with, and thus, show interference -- if two amplitudes differ in phase, the phase of the sum of the amplitudes is arrived at the same way as above, and may thus interfere constructively or destructively. The phasors discussed above can thus be represented very naturally as complex numbers; conversely, converse numbers exhibit the same phenomena we are already familiar with from phasors and their associated waves.
It is thus the different theory of probability, furnished by quantum mechanics, that is at the origin of the phenomenon of interference, and the apparent wave-particle duality. This is also the reason for the historically motivated terminology that refers to the state of a quantum system as its 'wave function', often denoted by the Greek letter ψ (psi), sometimes written as |ψ⟩, where the strange brackets just mean 'this is a quantum object'.
In the most familiar versions of quantum mechanics, there is a slight hitch here that I must confess I don't exactly know how to motivate using an intuitive argument. Basically, probabilities must be positive real numbers, so one takes the square of the absolute value of the amplitude in order to extract the physical prediction; this is known as Born's rule. This is not necessary in the two formalisms I have so far introduced: in doing quantum mechanics on phase space, the Wigner distribution yields probabilities in the same way as any ordinary probability distribution does, and in deducing quantum mechanics from quantum logic, the probabilities are obtained from the density matrices via a rule that is a natural generalization of the equivalent rule in classical probability theory. Of course, this rule is equivalent to the squared-modulus one, but it would take a bit of math to exhibit both in full detail -- it's important to note, however, that this is not an additional or ad hoc assumption in order to make things come out right, but a straightforward, if a little technical, consequence of the theory. For more technically versed readers, Saul Youssef has constructed an argument that this rule uniquely provides a relative-frequency interpretation of complex probabilities (see here).
The upshot of this is that it is now clear how to resolve the puzzles of the double slit experiment: the probability of any given point being illuminated is equal to the squared modulus of the amplitude for light to arrive there, which is equal to the squared modulus of the sum of the amplitudes for light to arrive there via slit 1 and light to arrive there via slit two. Or: P(x bright) = |A(x bright)|2 = |A(light through S1) + A(light through S2)|2. Since both amplitudes are complex numbers, they show interference, which is not changed by the squaring: if both sum to zero, then zero squared is still zero; if both sum to 1, the same holds, thus, there will be maxima and minima of illumination on the wall. Also, we immediately see the reason why the observation of light at the slits destroys the interference: the probability to observe light at any slit is equal to |A(light through S1)|2 or |A(light through S2)|2; thus, the observation having been made, the probability of light arriving at any point on the screen is equal to the sum of the probabilities of the light going there through either slit, thus: P(x bright) = |A(light through S1)|2 + |A(light through S2)|2. Since these are both positive real numbers, there is no interference, and we observe merely two bright bands behind the slits.
However, this should not be taken as an argument for an 'all particle' version of quantum theory -- the view that, say, an electron is after all a particle, and it is just the weirdness in the quantum mechanical probability that causes interference patterns to appear. Indeed, I am not sure if the question of whether the electron is a wave, a particle, both, or neither, is a sensible one to ask. After all, there are seemingly empirically adequate models in which it is either of those: in the de Broglie-Bohm or 'pilot wave' theory, the electron is a particle, albeit guided by a 'quantum potential', while Carver Mead has proposed a model of 'collective electrodynamics', in which only wave phenomena exist fundamentally, the discrete appearance of particles of matter being related to quantization effects.
Maybe this question is of the same kind as an inhabitant of the Matrix asking what programming language his world is written in, and what the program is that computes it: there can be no unique answer to it, as its object is not what one might call an 'element of reality' in somewhat antiquated terminology. The experimental phenomena are independent of whether the electron is a wave or a particle, just as the experience of a person living in the Matrix is independent of the implementation of his simulated environment. I've considered the question of what, in such a context, it is reasonable for scientific theories to address elsewhere.
The Path Not Not Taken
Let's recap: we have seen that, in order to explain the seemingly paradoxical behavior of light in the double slit experiment, it suffices to appeal to a generalized theory of probability, such that the observed interference effects are in fact due to the relative phases associated with each path a photon, i.e. a particle of light, can take to the screen. This led us to consider probability amplitudes, whose squared modulus gives us ordinary probabilities, and which simply have to be added in order to determine the total amplitude for a photon arriving at any given point on the screen.
About the double slit experiment, Richard Feynman, along with Einstein perhaps the most-quoted physicist of the 20th century, was reportedly 'fond of saying that that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment' (source). As we will now see, he had good reason to think so.
Consider, besides the first two, cutting another slit into the screen, for a 'triple-slit experiment'. Our prescriptions don't have to be changed: now, all that we have to do is to add three amplitudes in order to determine the likelihood of a photon hitting a given point on the wall. The same is true for four, five, six, etc., holes. Nothing qualitatively new emerges here.
Let's add a second screen behind the first one. Now we have a two-step process: in order to determine the amplitude for a photon hitting the wall, we must first consider the amplitude of it traversing the first screen, then the amplitude of it traversing the second -- i.e. in order to derive the amplitude of the photon, emitted at point A, arriving at some point B on the wall, we must sum over the amplitudes of the photon going through each hole in the first screen, then through each hole in the second, then to point B. Again, there is nothing qualitatively new here.
 |
| Fig. 12: Multiple slit experiment. |
But this actually exhausts the possibilities of modifying the experiment -- we can add more screens with ever more slits, but this will change nothing of the essence of our prior reasoning; we'll just have to evaluate ever more sums, which might get tedious, but does not introduce any new conceptual troubles.
So let's now consider the ultimate limiting case -- infinitely many screens with infinitely many holes in them. Clearly, we must sum over every path the photon can take to every point in between two points A and B, since at every point in space, there will be one of the infinitely many slits, and we have learned that we must sum over all slits. Again, this is nothing conceptually new (though in practice, things can get somewhat complicated when having to evaluate these infinite sums).
Now, the crucial thing to realize is that this case, in which there are infinitely many screens with infinitely many slits, is the same case as if there were no screens and no slits, but just empty space -- since at every point in space, there is a slit, and thus, at no point, there is a bit of screen. But this means, that in order to obtain the amplitude of a particle propagating from some point A to a point B, we must sum over all paths that it could take to get there, no matter how absurd they seem!
This is the germ of the idea behind the so-called path integral formulation of quantum mechanics, due to none other than Richard Feynman. (The above story is told in more detail, and with the math to back it up, in Anthony Zee's excellent Quantum Field Theory in a Nutshell, under the heading: 'The professor's nightmare: a wise guy in class'.)
Now, why do I introduce yet another formulation of quantum mechanics? There are two main reasons. First, the path integral formulation, while mathematically challenging, has the great virtue of lending itself well to intuition, better than other formulations at least. The second is that, using path integrals, or heuristic path sums, it is easy to show how quantum mechanics actually is necessary to establish a firm footing for classical mechanics, and to explicitly show the emergence of physical laws from a stochastic process, as discussed in the previous post.
To show this, I will borrow an example from Feynman's excellent 1985 popular science book 'QED: The Strange Theory of Light And Matter', which provides to this day the best introduction that I am aware of to the challenging concepts of quantum field theory, aimed at the general reader without mathematical background, showcasing Feynman's admirable skill at exhibiting high-level concepts without needing high-level mathematics. (The lectures the book was based on, by the way, are available as streaming video here.)
Let us consider the elemental phenomenon of reflection. Most readers will probably be familiar with the law that says that the angle of incidence has to equal the angle of reflection -- i.e. a beam of light, incident on a reflective surface under an angle α, will be reflected in such a way that the reflected beam will again form an angle of α with the reflective surface (or, as it is more usually defined, with a direction orthogonal to it).
The question is -- how does the light know to do this? Does it need to know in advance how the surface is tilted in order to be reflected appropriately? Is there a law that, from all possible angles of reflection, a priori selects the 'proper' one?
The answer can be found by thinking in sums-over-paths. The key is that the phase of every path depends on a quantity called action -- the larger the action, the higher the 'frequency', i.e. the faster the rotation of the little arrow in the phasor diagram. The action is a somewhat abstract quantity -- for our purposes, it is only necessary to know that it is dependent on the path the system takes.
Now take the following figure:
 |
| Fig. 13: Sum over possible reflection paths. Adapted from Feynman's 'QED'. |
It shows the phase and the action for different possible reflection paths. As you can see, the larger the action, the more the phases vary among adjacent paths. As we know by now, in order to get the total amplitude, we have to add the individual contributions, which can be done graphically:
 |
| Fig. 14: Sum of phases. Adapted from Feynman's 'QED'. |
There are three different regions to this diagram. The arrows in the middle one, labelled E to K, all point roughly in the same direction; their associated actions are small, so there is not much change in phase between the paths they represent. However, the arrows at the left and right ends, A to D and L to O, all point in progressively more different directions, leading to them 'going around in a circle'. But this means that their sum is equal to 0 -- they interfere destructively. Conversely, the arrows in the middle region reinforce one another -- they interfere constructively. The sum over paths will thus be dominated by those paths for which the action is small, since those paths get reinforced, while other paths get cancelled.
This is actually something quite remarkable: without putting it in, without postulating it, the law of reflection pops out, merely from the stochastic considerations on all possible paths of reflection! This law is thus a 'passive' one in the sense of the last post -- it is obeyed by the system, without having to be stipulated a priori; it is thus an emergent law.
But the consequences of this picture run much deeper than this. It can be used immediately to explain Fermat's principle, which says that 'light travels between two given points along the path of shortest time'. This principle, sufficient to explain all phenomena of reflection and refraction, poses, without the quantum-mechanical justification, a puzzle analogous to the previously formulated one: how can light know which path takes the shortest time to traverse? The answer is now clear: it actually traverses, in a manner of speaking, all possible paths -- but only those for which the travel time, and the action, is minimal, give a significant contribution!
But indeed, this is not yet the most general formulation. What holds for particles of light, in fact holds for all quantum mechanical systems -- in all cases, the 'path' (which may be more general than the notion of a single-particle path, i.e. a sequence of configurations of the system -- of some fields, say -- often more generally called a 'history') for which the action is minimal yields the greatest contribution to the amplitude -- so much so that, in the classical approximation (where quantum effects are deemed too small to care about), it suffices to consider only this path for the system. This is known as the least action principle, and it is arguably one of the most powerful tools in the toolbox of modern physics. (So much so that Bee Hossenfelder, over at Backreaction, has discussed it as a possible 'principle of everything', though simultaneously cautioning against the notion.)
The supreme importance of this principle can be gauged by realizing that all theories of modern physics, from Maxwell's electrodynamics to the quantum field theory (the already-mentioned QED or quantum electrodynamics) that encompasses it, from Newtonian mechanics to general relativity to the whole of the standard model of particle physics, can be derived through its application. One only needs some characteristic of the system one is discussing -- in the simplest case, its kinetic and potential energy --, and out pop the equations of motion, i.e. the laws governing the system's behavior. Since the principle of least action has its roots in the stochastic nature of quantum mechanics, thus all the laws of modern physics can be seen to be emergent ones -- eliminating the necessity of the laws being somehow set and fixed in an a priori way. Rather, they emerge from the behavior of the systems themselves.
As Bee notes, this is an enormously elegant tool for 'sensemaking': the universe follows the laws that it does, because of the principle of least action, because, in a sense, all possible laws a system could follow are implemented -- but only those that do not cancel each other out 'survive'. Thus, the laws emerge from lawlessness.
From Principle to Theory of Everything?
However, there is one question that is not addressed by the least action principle: while, given the particulars of a system, such as the universe, it can be used to derive the behavior of the system and the laws it follows, it is silent on why a system is the way it is, rather than some other way; this is generally considered as an input to be determined empirically. While it is possible that this is a hard and fast boundary, of either the principle or of science itself, the idea of extending its reach has been discussed occasionally.
Seth Lloyd, for instance, here considers the possibility of regarding spacetime as a computation, and answers the question of which computation is supposed to correspond to our particular spacetime by appealing to a superposition of all possible computations -- of all possible paths a computer might take through an abstract 'computational space'. This superposition is dominated by the programs with the shortest description -- by spacetimes with the smallest algorithmic complexity as discussed in this post. Thus, this produces a natural explanation for the fact that our universe seems to be governed by fairly simple laws -- these are the laws correspond to the shortest programs.
A related perspective is investigated by Jürgen Schmidhuber in his paper on 'Algorithmic Theories of Everything', and also by his brother Christof, who considers the possibility of deriving 'Strings from Logic'.
In such a picture, science would essentially be a process of data compression -- the effort to find the shortest program that gives rise to a certain set of data, in this case that data being the experience of the universe, concentrated into observations and measurements, since this program will be the one that dominates the 'sum over programs'. This is reminiscent of the tale of Leibniz and the inkblots, as told in the very first post of this blog: a couple of ink blots on a piece of paper may be considered lawful if they admit a complete description in such a way that the description is significantly shorter than just noting down the position of each blot -- i.e. if, for instance, there exists a short computer program that draws the distribution faithfully.
Also note the similarity of this construction to Chaitin's 'number of wisdom', the halting probability Ω, which is the sum of all halting programs on some computing machine, weighted by their length.
As a slight digression, this throws light on an aspect of science that is sometimes neglected: you can never be certain you have the complete picture. The reason for this is, quite simply, that compression isn't computable -- there is no universal program able to compute all strings by a maximal amount. So for each compression you find -- each candidate theory -- you will never be able to tell if it is the best possible compression; there always might be a better one lurking around. So the fun in science never ends!
Returning to the original point: there may be hope, if the universe is computable, to relate its complete description -- i.e. both its composition and the laws that it follows -- to a kind of 'least action principle' by considering all formally describable theories -- all possible computations --, which gives rise to a unique universe following a unique set of laws in the same sense that considering all possible paths gives rise to a unique path and angle of reflection for a beam of light. Such a universe would then be self-sufficient in the sense that neither its laws, nor its constituents, need any external justification -- they both emerge naturally out of the most general considerations possible.

Keine Kommentare:
Kommentar veröffentlichen